体验copilot
体验了一段时间的copilot,是时候来写个简单的总结了。
copilot是什么
copilot是一个vscode的插件。最初收到这个消息的时候,我就去申请参与内测,可能那时候已经晚了,一直等到公测才用上。它是一款自动提示插件,不过它的自动提示能力远超以前用过的,一用上,就把我惊艳到了,不是一般的函数名完成,或成员提示,而是一整段代码给你提示完成,甚至在尝试猜测你想要写的功能,直接给你补完一个函数甚至一个类。
先来看几个补全效果图:
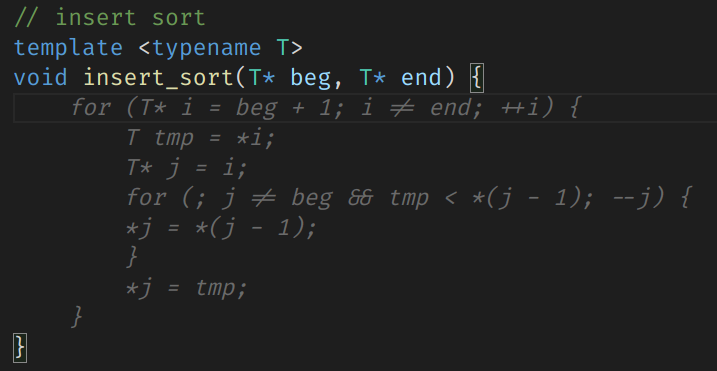
以上没有行号灰色部分就是自动补全的部分,你给出函数名,它就猜出你应该要的代码的效果,那以下来一个更复杂点的排序,当然也是没有问题的。
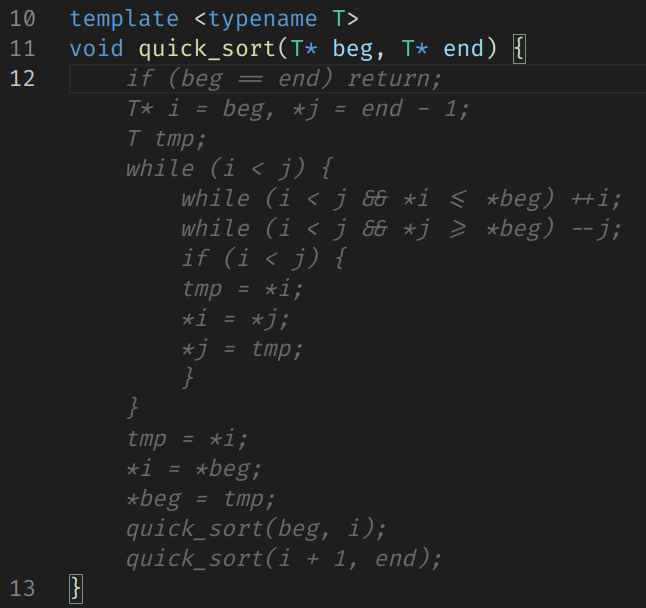
不止如此,你只要写上接下来的函数的注释,有一些它也能直接给你补完这个函数的实现,你的注释还能帮助它提供更准确的信息。所以这又一次说明注释的作用,不但是给人看的,不但是用来生成自动化文档的,甚至是用来自动生成代码的。
Read more...折腾NAND
近期在折腾SSD、SD、U盘,折腾差不多来写个总结,坑不少。本文部分内容会随着时间而变化,于2021年12月编写。
常见NAND硬件
用于储存的基于NAND的硬件,有SD卡、MicroSD卡,U盘,移动固态硬盘,固态硬盘,通常来说,SD卡这类体积小的速度最慢,U盘次之,再就是移动固态硬盘,最快是固态硬盘。之所以说通常,因为还要看接口和协议速度。
颗粒品质,原片、白片、黑片
储存颗粒按品质划分可以分为三大类,原片、白片、黑片。原片就是品质最好的,原厂最严格标准下的产品,白片就是从晶圆上不及格的里面,把还相对较好的挑选出来,黑片就是白片也不如,在剩下的挑选还能用的,同时把坏区进行屏蔽后造出来的颗粒,某宝上特别便宜的U盘肯定是黑片,还有像MP3,玩具等,通常都是用的黑片。黑片寿命说不准,快的一个星期,慢的2年,看运气。
颗粒类型,SLC、MLC、TLC、QLC、3D NAND
SLC表示,一个存储单元,只存0和1,即1bit,MLC保存00、01、10、11,即2bits,同理,TLC可以保存3bits,QLC保存4bits。SLC最贵,速度最快,寿命最长,可达10W次擦除(原片颗粒的情况下,不算白片黑片,下同)。MLC次之,约3000到5000次擦除。TLC再次之,约1000次擦除。QLC速度最慢,寿命最短,约800次擦除。另外,3D NAND可以大幅度提升寿命,3D TLC可达3000到5000次擦除,3D QLC可达1000到3000次擦除。
Read more...折腾linux
近期在折腾linux,折腾差不多来写个总结,这货折腾了我很长的时间。由于USB3.0已经发展很久了,现在随便买的MicroSD/SD卡或U盘基本上都是USB3.0 class 10起步,所以考虑直接用这些来安装系统,这样你对哪个系统不满意直接换个U盘或SD卡就搞定了,而且测试下来速度也不慢。即使你的机器只有USB2.0接口,那也是能用的,就是启动时能感觉出来慢一些。这个也是方便咱们在校学生只有一台电脑,能方便更换系统不必每次折腾一次硬盘,同时可以熟悉比赛时所用的linux环境。另外,如果你想偷懒,我在这也准备了一些系统镜像,直接刷入U盘即可使用,请参见本文最末尾。本文主要针对LTS20版ubuntu,存在有效时限。
在USB存储器上安装linux操作系统
在USB设备上安装个linux系统是很容易的,比起windows和MacOS来说,容易很多。这里有两种操作方式,一是使用虚拟机,这样我们只需要准备一个U盘(或SD或MicroSD卡,下文中说的U盘通常指这三者,且容量必须是16G或以上),二是使用真实机器来安装,这样我们需要准备两个U盘,多出来的一个是用来制作安装盘,安装工具推荐 Rufus 和 YUMI 以及 Ventoy,后两者可以用于制作多启动的U盘。
Read more...二分搜索杂谈
二分搜索虽然基本思想简单,但其细节却令人意外的抓狂(Although the basic idea of binary search is comparatively straightforward, the details can be surprisingly tricky)。这里我们来分析一下常见写法的坑。
两类不同的二分
二分有两类,一是找值,即判断某个值存不存在,二是找边界,前者比后者简单很多,以下是找值的典型写法(来自中文wiki百科)
int binary_search(const int arr[], int start, int end, int key) {
int ret = -1; // 未搜索到数据返回-1下标
int mid;
while (start <= end) {
mid = start + (end - start) / 2; //直接平均可能會溢位,所以用此算法
if (arr[mid] < key)
start = mid + 1;
else if (arr[mid] > key)
end = mid - 1;
else { // 最後檢測相等是因為多數搜尋狀況不是大於要不就小於
ret = mid;
break;
}
}
return ret; // 单一出口
}
对于找边界,有四种情况,如以下例子,查找数值5的四种边界
1 1 1 2 2 5 5 5 5 7 9
^ 1 小于的最右元素
^ 2 大于等于的最左元素
^ 3 小于等于的最右元素
^ 4 大于的最左元素
既然有四种边界,那就有四种写法。
Read more...大整数高精度计算3——快速傅里叶/数论变换及分治除法
在上一篇介绍了基础优化算法后,本篇介绍更复杂的内容。本篇的三大内容:FFT,NTT,分治除法。中文资料中我尚未发现有博客文章在介绍分治除法的,所以我就来写第一个介绍吧。
FFT (Schönhage–Strassen algorithm)
FFT就是快速傅里叶变换的缩写,FFT这里不重点介绍,参见oiwiki中对FFT的介绍
用比较显浅且简要的方式来介绍的话,FFT可以在$O(nlogn)$时间里(注:严格来说应该是$O(nlognloglogn)$,论文链接在这,在274页7.8处开始证明)求出两个多项式的乘积,而大整数乘法就可以视为两个整数系数的多项式的积再处理进位即可。那这样就产生一个问题,如果这个大整数采用的基数base,且长度为n,那么多项式的积的最大值可能会达到$n(base-1)^2$,因为FFT采用浮点运算,那么这个最大值必须在double的精度内,所以如果采用万进制,那么很容易导致精度不足进而结果错误,另外,还有求单位复根时的误差也会让它提早出现结果错误。实际应用的时候,一般采用10进制来增加长度的上限。所以如果你的大整数采用压位表示,那么在运用FFT之前,要先做拆位拆成10进制。总之,因为浮点精度的问题,不建议在大整数实现里使用FFT,建议采用下文要介绍的NTT来代替。所以这里对FFT的优化不做介绍,重心放在NTT上。
NTT
NTT就是快速数论变换,它和FFT很像,但它在整数域上做变换,具体数学介绍参见oiwiki中对NTT的介绍。由于没有浮点数参与,于是没有精度上的问题。
Read more...大整数高精度计算2——乘法优化及进制转换
在上一篇介绍了基础算法后,本篇介绍算法级别的优化。本篇的三大内容:乘法优化,任意进制输入,任意进制输出。
乘法优化
这里要介绍的,是Karatsuba发现的分治法,我们假设要相乘的两个数,都有2n位,那么这两个数就可以分别表示为$a_1base^n+a_2, b_1base^n+b_2$,其中,$a_1,a_2,b_1,b_2$是n位的大整数,那么,它们的积就是
$$\begin{align}
& (a_1base^n+a_2) \times (b_1base^n+b_2) \\
& = a_1b_1base^{2n} + (a_1b_2+a_2b_1)base^n + a_2b_2 \\
& = a_1b_1base^{2n} + ((a_1+a_2)(b_1+b_2)-a_1b_1-a_2b_2)base^n + a_2b_2
\end{align}$$
如果这样不够明显的话,我们用$c_1$代替$a_1b_1$,用$c_3$代替$a_2b_2$,得到
$c_1base^{2n} + ((a_1+a_2)(b_1+b_2)-c_1-c_3)base^n + c_3$
于是,这里一共有3次乘法,比起原来的4次暴力乘法减少了1次。而里面的乘法又可以进行递归优化,时间复杂度从$O(n^2)$下降到$O(n^{log_23})$约$O(n^{1.585})$
Read more...大整数高精度计算——有趣的实现
这里收录一些有意思的实现,不过我都有进行改编以更方便使用,不过千万不要指望这性能有多高。收录的条件:
- 支持四则运算,必须包含除法及求余
- 支持字符串输入输出
- 代码不长
small biginteger library for contest
代码原作者Jane Alam Jan,你可以在Google上直接搜索small_biginteger_library_for_contest.pdf并下载到原始说明文档及代码,这里提供一份代码,改动不多,增加了int的构造函数和其它不等号的重载,乘法效率有优化,且增加输出到string而不直接输出终端,以便在其它场合使用更方便。
大整数高精度计算1——基础算法
最近在编写大整数库的过程中,踩到不少的坑,于是把一些有用的细节准备写成文章做整理。如果你只是想直接查找并使用一个大整数库,那直接上GMP即可,如果是用在比赛,那直接用我的MiniBigInteger项目,如果你是想学习个中细节,那你可以坐下来细品。
所谓大整数,又叫高精度运算,就是运算对象是上千位甚至到百万位,总之远远超过内置数据类型的表示范围,这类数字都叫大整数。而C/C++的标准库里目前并没有大整数库,于是这个轮子被反复制造了无数个,不过在github上比较有质量的轮子并没有很多。本文除了介绍基础实现,主要还是介绍优化方法。
大整数的表示
大整数的表示方法最常见的有4种:
- 直接使用string
- 使用定长数组(仅适用于竞赛)
- 使用链表
- 使用变长线性表例如vector
直接用string的方式适合初学者,输入输出直观,但缺点也非常明显,因为计算时需要在字符与数值之间来回转换,浪费太多不必要的时间,效率会非常差。不过如果你是初学者,先用string表示法来写未尝不是个好主意。但有个细节就是,如果想要效率高,最好把string前后倒置调整为低位在前再做运算,这样速度和实现难度都会低一些。
至于使用链表,好处是变长容易,变短也不难,但性能比用string的更差还更难写,这里就不谈了,以下介绍使用数组的表示法
为了在数组里表示一个大整数,如果我们采用10进制,表示123456789,那很简单,例如这样:
很头疼拼图
本拼图难度较高,是给程序解答专用的题目(手工解我觉得没多少可能,但不排除有运气极佳的人),是检验你的程序效率有多高用的。
它的名字是很头疼拼图,因为放入的块有H和两种T形状,而HTT就是很头疼。一共有21个块,放入一个12x12的框里,具体形状如下图

以上是就是原题,每个小方块长宽均为1,底板尺寸是12x12。全部21块放入即成功解出,每一块均可以任意平移、旋转、翻转。你需要确定本题有多少个本质不同的解及相应具体答案。答案就不在这公开了,祝玩得开心。
Read more...Dancing Links 跳舞链
Dancing Links缩写为DLX,其实在竞赛中并不常见,这次会讲这个是因为前一阵子搞拼图写了这个数据结构就顺便写(水)博客。
DLX的发明者是高德纳(Donald Knuth),就是那个传说中的《计算机程序设计艺术》(TAOCP)系列书的作者,这里对这个算法做一些比较直观的解释。
DLX面向的问题
DLX面向的问题是精确覆盖问题。何谓精确覆盖呢,来看以下这个表格,每一行是一个数组,数组有4个元素,每行的第一列是这个数组的名字
| name | ||||
|---|---|---|---|---|
| a | 0 | 0 | 0 | 1 |
| b | 1 | 0 | 0 | 1 |
| c | 1 | 1 | 0 | 0 |
| d | 1 | 0 | 1 | 0 |
| e | 0 | 1 | 1 | 1 |
| f | 0 | 0 | 1 | 0 |
| g | 0 | 1 | 0 | 1 |
我们的目标是,在这些集合里,挑出几个,例如我们挑a,b,c,那对应位置上的元素相加,于是得到 2 1 0 2。而我们的目标是,找到一个挑选的方法,使得相加得到 1 1 1 1 全是1。
例如说,选 d和g,那么相加正好得到 1 1 1 1 ,这就是其中一个解,这就是精确覆盖问题的直观感知。