小恐龙拼图
本拼图难度较高,同时作为2021新年的起点!
它的名字是小恐龙拼图,因为需要连同右边小恐龙形状的拼图块一起放入,一共有11个块,放入一个12x12的框里,如下图

以上是就是原题,每个小方块长宽均为1,底板尺寸是12x12。全部11块放入即成功解出,每一块均可以任意平移、旋转、翻转。答案就不在这公开了,祝玩得开心。
Read more...101010拼图
前两个拼图最多算热个身,难度不高,真正有点挑战的是以下这个,作为2020的纪念
它的名字是101010,因为需要把10个块放入一个10x10的框里,如下图

以上是就是原题,每个小方块长宽均为1,底板尺寸是10x10。右边的块每一块都写了x2,表示有两块完全一样的形状,全部10块放入即成功解出,每一块均可以任意平移、旋转、翻转。答案就不在这公开了,祝玩得开心。
Read more...10个问号拼图
刷题经常搞得自己一脸问号,就想到弄一个由问号组成的拼图,如下图
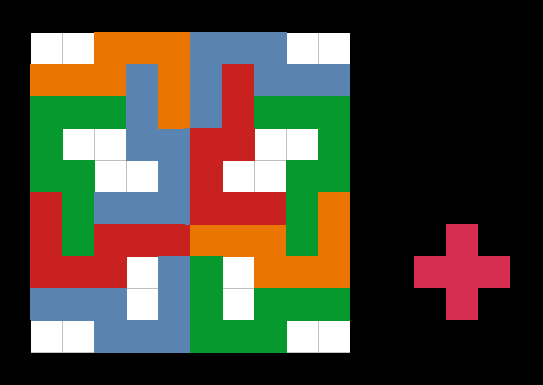
因为由10块一样的形似问号组合而成,所以我命名为10个问号。
以上是就是原题,不同颜色来区分不同位置的小块。每个小方块长宽均为1,底板尺寸是10x10。要求把右边的“十”无重叠放入到10个问号里,放入即成功解出,答案就不在这公开了,祝玩得开心。
Read more...Orz14拼图
为了表达对大佬的膜拜,特设计一款拼图,由14个近似Orz形状的小块组合而成,如下图

因为由14块一样的小块组合而成,所以我命名为Orz14,同时也有Orz一直到4的含义。
以上是就是原题,不同颜色来区分不同位置的小块。每个小方块长宽均为1,底板尺寸是11x11。要求把右边的绿色小块也一并无重叠放入,这一块就代表大佬,放入即成功解出,答案就不在这公开了,祝玩得开心。
Read more...解迷建模
这次来聊点简单的,也许你偶尔有机会在地摊上看到有人摆了一堆解锁玩具,这回我们通过建模来解决当中属于迷宫类型的玩具。
魔金·円


第一图是初始状态,第二图是解开后各自的形状。为了更能理解接下来我说的,最好当然是你手上有一个一样的。
但是,事实上可以存在两种不同的初始状态,其路线也略不相同,以下会做说明。
编码
稍微操作几下,我们就会发现,它的操作很简单,它的边缘有一上一下,在中间的孔也有一左一右,即边缘的宽度小于等于中间的孔时,就可穿过一格。我们把它如下图摆放(俯视图):

回文树
回文树(EER Tree,Palindromic Tree),有点类似Trie,但它并不是匹配字符串的,很多人称之为回文自动机,但它一点也不像自动机,不过我还是按习惯的来,使用PAM为简称。为了表示一个回文,我们只表示一边的一个单链即可,这时就类似Trie。但不同之处是,回文区分奇数长度和偶数长度,所以这里我们使用两个根,分别来表示奇数长度和偶数长度。所以,在奇数根里,链ba表示aba,而在偶数根里的ba表示abba。
首先我们来直观地看看PAM的图形化,以下是字符串abcbbc的PAM
graph TD;
linkStyle default interpolate basis
subgraph root
0-.->1[-1]
end
subgraph node0
0-->6((bb))
6-->7((cbbc))
end
subgraph node1
1-->2((a))
1-->3((b))
1-->4((c))
4-->5((bcb))
end
2-.->0
3-.->0
4-.->0
6-.->3
5-.->3
7-.->4
style 0 fill:#f9f
style 1 fill:#f9f
实线方向就是子节点方向,虚线是fail指针,指向这个节点最长的回文后缀节点。图有点乱,但又不希望画得过于简单导致说不清楚,将就一下吧。
Read more...后缀自动机SAM
后缀自动机(SAM),可以结合前文的AC自动机一起理解,所谓后缀自动机,就是把一个字符串的所有后缀构造AC自动机,即只匹配其后缀的自动机。但是作为一个字符串的所有后缀,与一般的AC自动机有些不一样的性质,直接构造AC自动机,节点数是 $O(n^2)$,而SAM则对重复的节点合并了,可以让节点数大幅下降到 $O(n)$。
首先我们来直观地看看SAM的图形化,以下是字符串abcac的SAM
graph LR;
linkStyle default interpolate basis
0((0))--a-->1
1--b-->2
2--c-->3
3--a-->4
4--c-->5((5))
0--c-->6(1)
0--b-->2
1--c-->5
6--a-->4
4-.->1
5-.->6
3-.->6
1-.->0
2-.->0
6-.->0
style 0 fill:#f9f
style 5 fill:#f9f
实线方向就是匹配方向,虚线与AC自动机中的失败指针非常像,在SAM里称为link指针。
Read more...AC自动机
听到AC自动机很多人第一次听到的反应往往是很兴奋的。但其实并不是你们想的那种东西。它的全称是Aho-Corasick algorithm,另外,自动机的英文是Automaton,所以AC自动机即 AC Automaton。为了解释这个算法,首先我们来回顾KMP,你需要很理解KMP的原理,不然看后面的内容就会变得妙不可读。
KMP自动机
本质上KMP其实就是一种自动机。这次我们改用自动机的形式来理解。所谓自动机,一般指的是确定有限状态自动机,你可以看作一个黑箱,每次输入一个数据,它就会改变它的内部状态,并有相应的输出。如果你知道Trie,那么它其实就是一个典型的自动机。我们还是拿字符串abacabab作为例子,如果是生成next数组,结果如下:
| string | a | b | a | c | a | b | a | b | \0 |
|---|---|---|---|---|---|---|---|---|---|
| next | -1 | 0 | 0 | 1 | 0 | 1 | 2 | 3 | 2 |
为了方便变成自动机的方式理解,我们把这个改成有向图
graph LR;
linkStyle default interpolate basis
0[Start]--a-->00[1]
00--b-->1[2]
1--a-->2[3]
2--c-->3[4]
3--a-->4[5]
4--b-->5[6]
5--a-->6[7]
6--b-->7[8]
00-.->0
1-.->0
2-.->00
3-.->0
4-.->00
5-.->1
6-.->2
%%7[b]-.->3[c]
style 0 fill:#f9f,stroke-dasharray: 5, 5
style 7 fill:#f9f,stroke-dasharray: 5, 5
伪随机数生成算法
这次主要介绍伪随机数生成算法,顺便介绍一个在2018-2019年的伪随机数研究成果,就是 xoshiro/xoroshiro 随机数生成算法。
历史
在较早的时候,甚至到现在,伪随机数的生成元老级别算法“线性同余伪随机数生成算法”可谓无处不在,像现在的C/C++的rand函数就是使用线性同余实现的伪随机数生成。所谓的线性同余法,就是这个迭代方程 $S_n = (aS_{n-1} + c)\mod m$,其中,$S_0$ 称为这个随机序列的种子,a,c,m是三个常数,不过这三个数不能随意选,m的大小决定随机数的周期,最大周期等于m,为了便于在计算机里实现,通常m选取$2^{32}$或$2^{64}$。在m已经确定为这两的时候,为了让周期尽可能大,常数a,c还至少要满足以下条件:
- 若 c 非 0,那么 c 与 m 互质;若 c 为 0,那么 a 与 m 互质
- m 所有的素因子均能整除 a-1
- 若 m 是4的倍数,那么 a-1 也是 4 的倍数
- a 和 c 都是正整数且小于 m
一些典型的常数取值可以参见wiki上的线性同余条目。
更高的需求
我们之所以使用线性同余,就是因为它实现简单,在对随机数质量要求较低的时候,例如用来作为treap的随机数,那么线性同余完全够用,但建议不要使用rand,因为在windows下不少编译器的最大值太小了,导致效果下降,自己写一个用参数a=69069,c=1,m=2^32比rand好,我在那篇关于treap的文章就是用了这组参数。线性同余法最大的缺陷是低位随机性特别差,如果使用类似next() % k的方式来获得区间在$[0,k-1]$的随机数,那么当线性同余迭代方程的m是2的幂且k也是2的幂的时候,灾难就发生了,特别地当k是2的时候,你将得到一个0101的循环序列。为了避免这种情况,通常会取线性同余结果的高位,而且低位去掉得越多,%2的周期就越长。例如结果是64位,取高32位作为最终结果,那么%2的周期就是 $2^{33}$ ,但这样会导致有效位减少,而且问题也没有根本地解决。另一种解决办法是选取一个素数作为m,例如2147483647正是一个素数,但如此一来,线性同余的计算速度就会慢不少,周期也没有前一个的长。两种基本实现如下:
可持久化线段树
可持久化权值线段树,wiki上指出引入者名字叫黃嘉泰,名字缩写正好是某位主席名字,所以又叫做主席树。而本篇先介绍可持久化线段树,阅读本篇前你需要先了解线段树
概念
所谓的可持久化,意思是你能得到所有的历史版本,为了达到这个效果,当然可以每次修改的时候,先整体复制再修改,结果自然就是会爆内存。而事实上,由于每次修改最多改一条链,而其它分支可以重用。我们先拿链表做例子,如果有个链表内容是 1->2->3->4->5 ,现在我们把3修改成6,得到 1->2->6->4->5 ,但是后面的元素没有改动,所以我们可以把后面的元素直接重叠在一起使用,如下图:
graph LR;
1-->2
2-->3
3-->4
4-->5
1'-->2'
2'-->6
6-->4
这样,完全可以当成两条不同的链表使用,同时节省空间。而可持久化线段树做法与这一样,就是没变的部分还使用原来节点,所以这个实现不能使用之前介绍的堆式储存,要和平衡树一样动态开节点。
数据结构
假设我们的数据是以下这样
| 下标 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| 数据 | 1 | 0 | 5 | 2 |
构建线段树后结果如下
graph TD;
1,4:8-->1,2:1
1,4:8-->3,4:7
1,2:1-->1,1:1
1,2:1-->2,2:0
3,4:7-->3,3:5
3,4:7-->4,4:2
冒号前面的两个数表示一条线段,冒号后表示的是数据,这个数据表示的是这个区间的和。
然后我们要把第3个元素从5改为1,构造第二棵线段树,首先复制一个root,包括儿子的指向也复制,得到
graph TD;
1,4:8-->1,2:1
1,4:8-->3,4:7
1,2:1-->1,1:1
1,2:1-->2,2:0
3,4:7-->3,3:5
3,4:7-->4,4:2
1,4':8-->1,2:1
1,4':8-->3,4:7