解迷建模
这次来聊点简单的,也许你偶尔有机会在地摊上看到有人摆了一堆解锁玩具,这回我们通过建模来解决当中属于迷宫类型的玩具。
魔金·円


第一图是初始状态,第二图是解开后各自的形状。为了更能理解接下来我说的,最好当然是你手上有一个一样的。
但是,事实上可以存在两种不同的初始状态,其路线也略不相同,以下会做说明。
编码
稍微操作几下,我们就会发现,它的操作很简单,它的边缘有一上一下,在中间的孔也有一左一右,即边缘的宽度小于等于中间的孔时,就可穿过一格。我们把它如下图摆放(俯视图):

这两个disks都有一个特点,有一个孔特别长,这两个孔交错时为初始位置。我们把这个特殊的孔编号为0,然后这个孔中间一左一右大小不同,我们按小的为主方向,于是上图左边的disk从0号孔开始顺时针编码1到6,右边的disk从0号孔开始也是顺时针编码1到6。由于都是顺时针,我称它为同向的初始状态(还有一种是反向的)。
再来看,左边的disk从0孔到1孔顺时针方向的边是粗的(如下图红色圈),但右边的disk从0孔到1孔顺时针方向的边是细的(如下图蓝色圈),这也决定这两个disk是不同的,在这规定顺时针方向下粗的是disk a,细的是disk b,且a总是放左边,b放右边,如图的交错方式

观察完毕后,为了方便写成代码,我们开始对disk a进行状态描述,如下图,对孔1为例子,取它的顺时针方向的边与它作为一组,按图上次序编码,窄的为0,宽的取1

最后按定义好的方向,进行编码,得到如下的编码表:
int disk_shape[2][7][4] = {
{
{1, 0, 1, 0},
{0, 1, 0, 1},
{1, 0, 1, 0},
{0, 1, 0, 0},
{1, 0, 0, 1},
{1, 0, 1, 0},
{0, 1, 0, 1},
},
{
{1, 0, 0, 1},
{0, 1, 1, 0},
{1, 0, 0, 1},
{0, 1, 0, 0},
{0, 0, 1, 0},
{1, 0, 0, 1},
{0, 1, 1, 0},
},
};
有了编码,接下来的事情就是判断哪些位置能做操作了。对于每一个位置,我们都有对disk a顺时针和逆时针,对disk b顺时针和逆时针共4种操作,那直接写成代码并打印,看看哪些可以即可。
具体代码
#include <algorithm>
#include <cstdio>
int st_map[7][7][4];
void genmap()
{
int disk_shape[2][7][4] = {
{
{1, 0, 1, 0},
{0, 1, 0, 1},
{1, 0, 1, 0},
{0, 1, 0, 0},
{1, 0, 0, 1},
{1, 0, 1, 0},
{0, 1, 0, 1},
},
{
{1, 0, 0, 1},
{0, 1, 1, 0},
{1, 0, 0, 1},
{0, 1, 0, 0},
{0, 0, 1, 0},
{1, 0, 0, 1},
{0, 1, 1, 0},
},
};
for (int dl = 0; dl < 7; ++dl)
{
for (int dr = 0; dr < 7; ++dr)
{
char s[5] = " ";
// 反向
/*
if (disk_shape[0][(dl + 0) % 7][2] <= disk_shape[1][dr][1] && disk_shape[0][(dl + 0) % 7][3] <= disk_shape[1][dr][0])
s[0] = 'D', st_map[dl][dr][0] = 1;
if (disk_shape[0][(dl + 6) % 7][2] <= disk_shape[1][dr][1] && disk_shape[0][(dl + 6) % 7][3] <= disk_shape[1][dr][0])
s[1] = 'U', st_map[dl][dr][1] = 1;
if (disk_shape[0][dl][0] >= disk_shape[1][(dr + 0) % 7][3] && disk_shape[0][dl][1] >= disk_shape[1][(dr + 0) % 7][2])
s[2] = 'R', st_map[dl][dr][2] = 1;
if (disk_shape[0][dl][0] >= disk_shape[1][(dr + 6) % 7][3] && disk_shape[0][dl][1] >= disk_shape[1][(dr + 6) % 7][2])
s[3] = 'L', st_map[dl][dr][3] = 1;
//*/
// 同向
//*
if (disk_shape[0][(dl + 0) % 7][3] <= disk_shape[1][dr][1] && disk_shape[0][(dl + 0) % 7][2] <= disk_shape[1][dr][0])
s[0] = 'D', st_map[dl][dr][0] = 1;
if (disk_shape[0][(dl + 6) % 7][3] <= disk_shape[1][dr][1] && disk_shape[0][(dl + 6) % 7][2] <= disk_shape[1][dr][0])
s[1] = 'U', st_map[dl][dr][1] = 1;
if (disk_shape[0][dl][0] >= disk_shape[1][(dr + 0) % 7][2] && disk_shape[0][dl][1] >= disk_shape[1][(dr + 0) % 7][3])
s[2] = 'R', st_map[dl][dr][2] = 1;
if (disk_shape[0][dl][0] >= disk_shape[1][(dr + 6) % 7][2] && disk_shape[0][dl][1] >= disk_shape[1][(dr + 6) % 7][3])
s[3] = 'L', st_map[dl][dr][3] = 1;
//*/
printf("%4s,", s);
}
puts("");
}
}
int main()
{
genmap();
return 0;
}
于是UD对应disk a的操作,LR对应disk b的操作
结果
我把运行结果导入到表格并对可移动的路径进行染色,结果如下(黄色的是起点和终点状态,深绿色是最短路径)
同向

反向
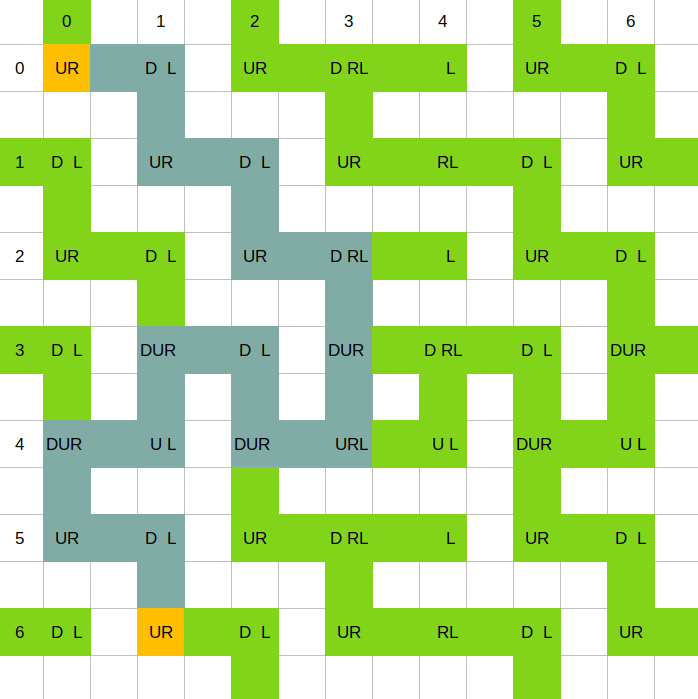
接下来的事情就简单了,路径明显不唯一,只要按定义操作,怎么走都可以,两种方向均最短15步。
魔金·磁


它也是个迷宫,它有两个小环,开口处有一边有个小齿,这导致了这两个小环的路线是不一样的。
编码
首先,小环横跨两个区域,那么我们对区域进行编号,且规定图上可见的面为正面

然后,两个小环规定,齿在正面时,开口所占区域为十位,另一区域为个位,于是,初始状态分别是09和90(十位的0不能省略)
但是这个由于比较复杂,编码的时间可能比手动列出状态还麻烦,所以我直接手动把所有的状态做成表格
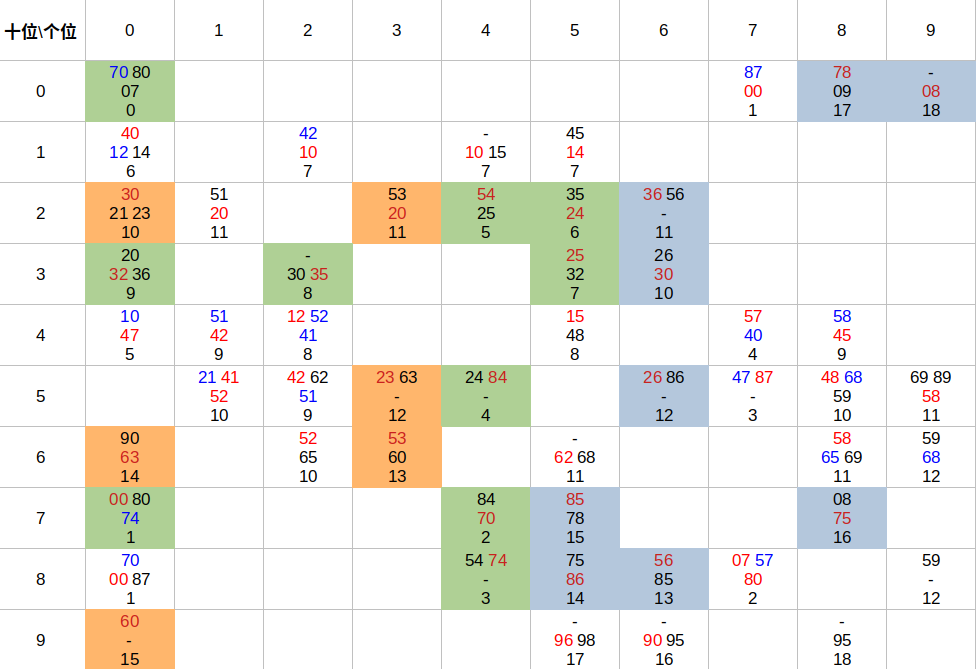
表格中前两行,表示该状态可以跳转到哪些状态,第三行表示该状态距离解出还需要的步数。每一格的红色数字表示向此数字走能最快到达出口。蓝色表示向还原的方向,没有蓝色时按红色数字的方向。
特殊情况是30这个状态,即第三行第0列,它移动到20或36,分别能移动到两种不同的初始状态。
蓝色和橙色格子表示两条不同状态的路线,而绿色表示这两条路线的公共部分。
但是,记忆这个表太难,且操作起来不是太舒服,唯一好处就是任意情况都能处理。为了快速解开或复原,我加了一个方便操作的数字串:
解锁:
90:6-3-52-0-3- 25-2-4-587-0-0
09:-8-7-5-8-6-523-0 25-2-4-587-0-0
还原:
90:7-4-852-5-3-20 -2-3-56-0-9
09:7-4-852-5-3-20 6-258-5-7-8-0-9
规定初始状态是小环开口小齿在正面,减号表示小环自身转90度,数字表示移动小环其中一则到此区域。
最后
这种方法只能对比较规范的puzzle进行建模,我看到网上似乎没有针对这两而做的解法视频,所以我就做了一个建模版本,把路线图形化,这样比起单纯一个正解视频,你可以知道任意情况下怎么解,这个是优点。不过缺点是你得花点时间去理解它是怎么编码的。好久没更新了,所以来写点特别的。